昨日、こんな記事を見つけました。
“三角形の面積”小6の正答率2割、専門家「衝撃的」 全国学力調査
https://news.livedoor.com/article/detail/24714252/
テープを直線で切って作った二つの三角形の面積についての問題。正答率は21.1%にとどまった。
さらに、このような話題も見かけました。
こちらは、とある大学で数学を教えていた大学教員が実際に経験したお話のようです。内容を一部抜粋してみます。
実は昔、とある大学で『数学』の授業の非常勤を数年したことがあるのですが、内容はほぼ算数でした。
その初回でいくつか問題を出して、そのうちの一つが「1000円の2割引はいくらですか」という問題でした。
そのプレテストの解答の中には、
「1000−2=998円」
「1000÷2=500円」
「2割=0.2である。よって
1000÷0.2=5000円」
という解答もありました。
割合というものを理解せずに大人になると、こういう風になるんだなぁ、というのを目の当たりにした感じでした。もちろん、速さなんて理解してなくて「時速4kmで2時間進むと、何km進みますか」という問いに対しても、多くの学生が「はじきを忘れたので、解けません」でした。
彼らも、数の計算ができないわけではないのです。例えば、280×3.2を計算してといえば、計算できます。しかし、数直線を書いて、100、200、300、という目盛をつけたあと、280はどこ?(これは分かる)を確認したあと、280×3.2はどのあたり?と聞くと、「そんな難しい計算はやってみないと分かりません」というんですね。
大事なことは計算の練習ではなくて、割合の表現が何を意味しているかの理解なんですね。そんな彼らに、つまづいてしまったところからきちんと授業しました。ちゃんと、教えれば分かるんです。
両方ともかなり衝撃的な内容ですが、この2つに共通することは、
「概念の理解を疎かにして、公式の使い方を意識させた結果、悲惨な状況になっている」
ということでしょう。
公式の使えるようになることよりも概念を理解することの方が重要であるという話は以前、ブログ内で書きました。
さて、「とりあえず公式を使って答えが出せることが大切。理解は後からついてくる」とおっしゃっていた学校教員や塾講師の皆さん、お元気ですか???こういうお話を聞いて一体どう思われているんでしょうね??
ほんと、理解がついてくるのは一体いつなんだよ!?って話ですよね。少なくとも上の大学教員の体験談においては、間違った学習観のまま勉強を続けてきた子達が、割合の正しい概念を身につけるということは大学生まではなかったようです。
最初の記事にしても、概念の習得はそっちのけで、公式の使い方にばかり注力してきた結果でしょうね。
教育心理学の研究を探せば、「解き方を天下りで覚えさせた場合と自分で考えさせた場合で、前者は短期的には点を取れても長期的にはデメリットの方が大きい」という報告はたくさん出てきます。たとえばこんなの。
面白いのは、「勉強が苦手なグループほど『自分で考えさせた』ことによる効果が高かった」と報告されている点でしょうか。算数がわからない・苦手という生徒に「とりあえず理解していなくても解ける方法を覚えさせる」方針は逆効果だそうです。よって、
高校で数学が苦手にならないための秘訣は、公式の成り立ちの理解に時間をかけるのではなく、
公式の使い方に時間をかける😃
です❗️
延岡の某学習塾ブログより一部抜粋
という、数学が苦手な子をさらに苦手にする最悪なやり方をブログで、ドヤ顔でオススメしちゃうような塾にはまず間違いなく行かない方が賢明というものです。
理解を伴わない学習にデメリットが多いなんてことは、ほぼ自明な気もするんですが、おそらく教える側もそういう質の高い勉強をしたことがないのでわからないんでしょうね。そして、お粗末な「ぼくの考えたさいきょうのやりかた」によって生徒たちの考える力を破壊しているわけです。
つまり、ほとんどの学校教員や塾では、典型問題を大量に解かせて丸暗記させてパターンマッチングで解かせるようなことをやってるわけです。そんなんだから苦手になるんです。できなくなるんです。いかに公式暗記が無意味かということは、上のお話を見れば一目瞭然でしょう。高校受験で一番気をつけないといけないのはここなんです。それもブログ内で既に言及してます。
何回も繰り返しますが、大事なのは、公式の使い方を覚えるのではなく、自分の頭でしっかりと考え、概念を理解することです。
概念を理解してるっていうのは、三角形の面積の公式を知らずとも、「底辺」や「高さ」という言葉を知らずとも、自分で考えて導けるという状態が出来ていることを指します。ここら辺も勘違いしている人が多いですが、三角形の面積は公式があるから求められるというわけではないですよ?
三角形の面積は、長方形→平行四辺形の面積の半分と捉えられることが本当に理解しているという状態なんです。それに、何やら一部の頭の弱い教員や塾講師は「底辺×高さ÷2という順番で立式しなければ×だ!」という頓珍漢なことを言っているようですが、高さや底辺なんてのは見方によるわけで、順序はどちらでも良いし、なんなら底辺だの高さだのは、公式を表現するための便宜的なものに過ぎないので、面積が求められるなら、「高さ」「底辺」という言葉を知らなくてもかまわないわけです。そんなことは本質ではない。
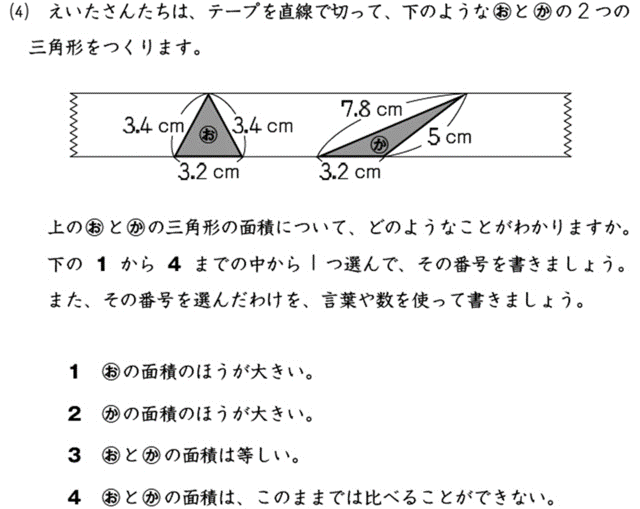
少なくとも、もし順序が逆だとダメだというならその反例を示すべきですね。まぁ、そんな本質ではない枝葉のところばかり気にして指導しているから、三角形の面積すら出せない小学生が多く生まれるんですよね。以下の問題は令和3年の学力調査の問題ですが、なんと正答率55%らしいです。
底辺×高さ÷2の順だと言ってる教員はこれどうするんでしょうかね?(笑)どんな風に解くのか見てみたいものですね。
公式が与えられて、それを言われた通りに使うのが算数や数学というのは間違いです。公式は定義や他の定理から導かれる単なるショートカットに過ぎないわけで、なぜそんな結果が出てくるのかというところの理解こそが大事です。そして、これをすっ飛ばしてしまうと、後から理解がついてくるということは決してないのです。